
 双眼鏡、望遠鏡の種類と原理
双眼鏡、望遠鏡の種類と原理
望遠鏡は遠方の物体を拡大して観察する光学器械です。
望遠鏡を大別すると下表のようになります

1.双眼鏡の種類と原理
 プリズム双眼鏡の原理
プリズム双眼鏡の原理
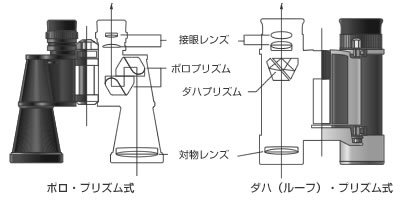
対物レンズ、接眼レンズともに凸レンズを使いますと、像が倒立し左右が反対に見えてしまいます。これを正立させるために、ポロプリズム、ダハ(またはルーフ)プリズムを使用している双眼鏡をプリズム双眼鏡と称します。多くの双眼鏡はこのタイプで作られています。(図1・図2)
図1 図2
 ガリレイ双眼鏡の原理
ガリレイ双眼鏡の原理
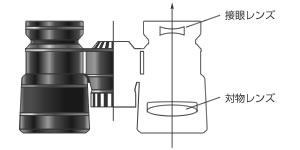
接眼レンズに凹レンズを使用している、オペラグラスとも呼ばれる簡単な構造の双眼鏡です。このタイプの双眼鏡では、倍率を高くしたり、視界を広くすることは困難であり、一般に、倍率は2.5倍から4倍程度で、小型のものが多く、観劇など屋内催事向きと言えます。(図3)
図3
2.天体望遠鏡と地上(単眼)望遠鏡の種類と原理
 屈折望遠鏡の原理
屈折望遠鏡の原理
屈折望遠鏡はケプラー望遠鏡が一般的です。
このタイプの望遠鏡では、太陽や月のような物体を見る場合、そこからくる光線は光軸と平行であり、像を結びますが、周辺からくる光は光軸に対して傾斜して入ってきます。
図1に示すように遠方の物体PQのQすなわち光軸からすこし離れたところから出た光は、対物レンズを通ったあとQ’に像をむすび、PQの実像がP’Q’に出来ます。
Q’から進んだ光は接眼鏡に入ってから図のような光路で出て行きますが、この光が目の瞳孔に入ると接眼レンズL2は虫めがねと同じ原理ではたらき、P’Q’をP”Q”に拡大し、見ることができます。つまり遠方の物体を対物レンズの中心Oから見たときの視角∠POQが望遠鏡をとおして見た場合は、視角∠P”EQ”となって肉眼で直接PQを見るよりはるかに角度(視角)が大きくなり、したがって物体が大きく見えるわけです。
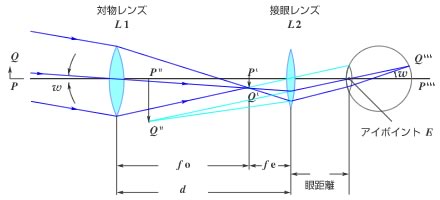
図1
対物レンズと接眼レンズの間隔 d は両レンズの焦点距離 f0 と fe との合計、d = f0 + fe となり、観察される像は倒立像となる。対物レンズには像の色のにじみをなくすため、2種類のガラスを組み合わせたアクロマートレンズ(色消しレンズ)が使われています。
 反射望遠鏡の原理
反射望遠鏡の原理
反射望遠鏡の形式としてはニュートン式、カセグレン式が一般的です。
ニュートン式、カセグレン式とも中央のへこんだ凹面鏡(放物面)によって 光を集めます。
凹面鏡で集められた光はニュートン式では45°に傾けられた平面鏡(斜鏡)でさらに反射して光を筒の外に出します。これを接眼鏡レンズで拡大して見ます。
またカセグレン式では凹面鏡からの光は副鏡(双曲面鏡)で焦点距離が引押されて集められ、接眼レンズで像を拡大して見ます。カセグレン式の利点は鏡筒を短くできることです。
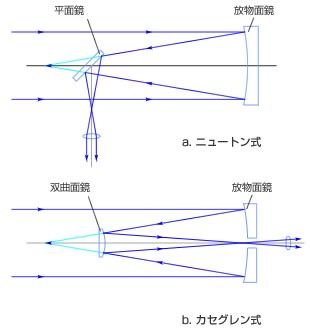
図2
 地上(単眼)望遠鏡の原理
地上(単眼)望遠鏡の原理
ケプラー望遠鏡は地上観察用としては倒立像望遠鏡であるので不都合です。
そのためケプラー望遠鏡で対物レンズと接眼レンズの間に正立レンズあるいは 正立プリズムを挿入し、正立像望遠鏡とします。これが一般地上観察に用いられる地上望遠鏡です。
正立レンズを組み合わせた形式は、図3のとおりで対物レンズL1により結像された像yは正立レンズにより上下左右反転されて、ふたたび結像し、接眼レンズL2により観察されます。そして出射光の角w′は入射光の角wと同方向となり、観察される像は正像となります。
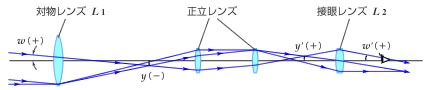
図3
正立プリズムも正立レンズと同様の作用があり、もっともよく用いられるのがポロプリズム1型および2型です。
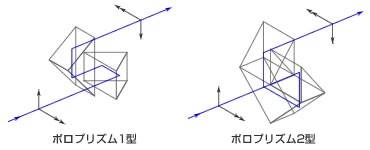
図4 ポロプリズム
 双眼鏡、望遠鏡の仕様性能
双眼鏡、望遠鏡の仕様性能
倍率、視界、明るさ(ひとみ径)および分解力や収差の程度が双眼鏡や望遠鏡にとって重要な仕様性能です。中でも天体望遠鏡は主として無限遠の星の観測に用いられるので、その口径が集光力と分解力を定めるので特に重視されます。
 倍 率
倍 率
倍率は、肉眼で見たときの物体の大きさと、双眼鏡でのぞいたときの大きさの割合であらわします。例えば、7倍の望遠鏡では、肉眼で見たときよりも7倍大きく見えます。これは、言いかえると、700m遠方の物体が、100mに近づいて見えるとも言えます。
見方を変えれば、望遠鏡をとおして見たときの物体像の視角ω′と直接見たときの物体の視角ωの比でもあります。
この場合、倍率をmとすると下式であらわされます。
ここに対物レンズ、接眼レンズの焦点距離をf0、feとします。
m=tanω’/tanω 、 m=- f0/ fe
ここでm>0のとき正像、m<0のとき倒像です。
また、地上単眼望遠鏡や双眼鏡の倍率は対物レンズ有効径とそれに対する射出ひとみ径との比でも求められます。
(例)
| 倍率(7倍)= | 対物レンズ有効径 50mm |
| ひとみ径 7.1mm |
 視 界
視 界
視界には実視界と見掛け視界があります。
・実視界(物体空間の視野角)
双眼鏡で見える範囲を、双眼鏡を介さずに見た場合の視界角度を実視界と言います。
・見掛け視界(像空間の視野角)
双眼鏡の光学系がつくる見掛の像の大きさを、角度表記したものを見掛け視界と言います。
即ち、見掛視界とは実視界の望遠鏡に入射する角2wが接眼レンズを出射するときは拡大して2ω’となり、この2ω’をいいます。
実視界 2ω、見掛け視界 2ω' および倍率Γとの関係は、次の式で表されます。
tan ω' =Γ × tan ω
例えば(図5)の場合、次のような関係式となります。
tan 23.5°= 7 × tan 3.55°
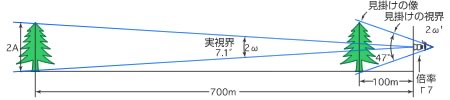
図5
<tanω’=Γ × tan ωの解説>
2ω =実視界、2ω’=見掛け視界、2A =700m先の視界 と定義する
まず実視界については、
tan ω=A/700・・・(1)となる
また見掛け視界については、
tanω’=A/(700/Γ)・・・(2)となる
*但し、700/Γは見掛けの像までの距離(倍率分だけ近くに見える)
(2)よりtanω’/Γ=A/700・・・(3)となる
(1)と(3)より
tanω’=Γ×tan ωとなります。
近似的には、2w′=m2w となり、見掛視界は実視界と倍率の積です。
 ひとみ径
ひとみ径
望遠鏡における明るさはひとみ径の大小によって定まります。
接眼レンズをレンズから目をはなしてみると円形の像がえられます。
これは対物レンズの接眼レンズによる像で、アイリングとも呼ばれます。
この円形像の直径をひとみ径といいます。望遠鏡の明るさはこのひとみ径の2乗に比例します。従って、ひとみ径が大きいほど明るい双眼鏡となります。
このひとみ径は次の関係式で求められます。
ひとみ径=対物レンズの有効径/倍率
(双眼鏡での例)
7×50の場合の明るさ
ひとみ径(7.1mm)=対物レンズ有効径(50mm)/倍率(7倍)
明るさ 7.12=50.4
7×35の場合の明るさ
ひとみ径(5mm)=対物レンズ有効径(35mm)/倍率(7倍)
明るさ 52=25
従って、7×50は、7×35の2倍明るいことになります。
人の目のひとみは昼間は2~3mm,夜間は7~8mmにもなります。
望遠鏡による光量の損失が少ないとすると、望遠鏡のひとみ径が観察者の目のひとみ径より小さければ暗く感じ、大きいときは目のひとみの大きさで絞れるので直接観察するときと同じ明るさとなります。上記の例のように、射出ひとみ径7.1mmの7×50が、明るい双眼鏡と言われる理由がここにあります。夕暮れなど光量の少ないときや暗いところでは、ひとみ径の大きい双眼鏡が適します。
ひとみ径は正式には接眼レンズ側にダイナメータという測定器を使用して測定します。
 分解力
分解力
物体の細部がどの程度まで鮮明に見分けられるかと言う、双眼鏡の解像能力を分解力といいます。
分解力は、相接近した2点の識別能力で、2点間の角度で表されます。
人の眼の分解力は、60”とされています。それは、網膜の円錐視細胞の単位面積の数等により割出されたものです。双眼鏡を通して物体を見る場合、倍率を上げた分だけ分解力を増すことができます。
即ち、 60″(人の眼の分解力)/10×(10倍双眼鏡)=6″
しかし、同径の対物レンズで倍率を上げていっても回折現象(光の特性)のため、おのずと限界(ドーズの限界)を生じ、ある程度以上の分解力を高めることはできません。分解力は基本的に対物レンズの口径によって定められ、大きさに比例して良くなります。口径に対する分解力の上限を「ドーズの限界」といい、実験的に116を対物口径で割った値とされています。
例えば、口径80mmの対物レンズは、およそ1.5”
口径50mmの対物レンズは、およそ2.3”
人の眼は、前述の通り60”です。従って上記の50mmの対物レンズは、計算上60”÷2.3”=26で、26倍が有効倍率と言えます。が三脚等で固定し明るい物体(明所視)を楽に見るために、さらに倍率を高めた方が見やすくなる場合もあります。
対物有効径が70mm、80mmの大口径双眼鏡が、船舶や観光用に使用されているのは、遠方の物体や景色の識別能力がすぐれているからです。
分解力は地上単眼望遠鏡と天体望遠鏡では測定方法が異なります。
(4-1) 地上単眼望遠鏡の分解力
地上単眼望遠鏡の分解力は、分解力テストチャート(白線、黒線が交互に並んだもの) を用います。分解力はテストチャートの一組の縦および横の縞模様のうちで同時に見分けることが出来る最小の白黒パターン値で表わします。
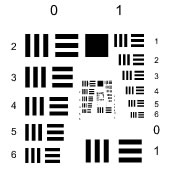
図6
(4-2) 天体望遠鏡の分解力
天体望遠鏡の分解力は、光学系を通して2点を2点として見分けることが出来る能力を分解力といいます。測定装置を通して、テストチャートの点像が確実に分離する値を測定します。接近した2つの点をはっきり2点として見分けられる能力(最小視角)を分解力といいます。但し、回折の影響等も含めて検証しております。
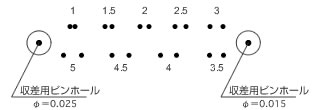
図7
 収 差
収 差
収差にもいろいろな種類がありますが、ここでは双眼鏡において大事な歪曲収差について説明します。
双眼鏡の倍率を高くしようとすると、光学的性能が劣る場合が生じます。手ブレ等によって見にくくなるのもその一因です。一般的に5~10倍程度が使い勝手が良く、まず平面的な目標(ビルの窓、近いところではカレンダー等)をとらえて比較することです。見える像の周辺の歪みが大きいもの、周辺のボケが著しいもの、細かい文字等がチラチラして定まらないもの等、判別する基準になります。
レンズには、いくつかの収差といわれるくせがあって、その全部を除去できませんが、良い材料、高精度研磨、正しい設計によって、正確につくられたものが良い双眼鏡といえます。
収差の一つの例を示すと、図8の左図のように像が著しく歪曲する場合を考えますと、これは中心部より周辺の倍率が大きく像のゆがみが生じたためです。自然現象では起き得ない未知との遭遇にともどった視細胞が脳を混乱させて不快感を起こすのです。
ある人は、人の眼は一点にしか神経を集中できないので、双眼鏡の像は中心だけ良ければ視界の周辺が悪くてもさしつかえないと言います。これは大変な間違いで、ふだん網膜には収差のない完全な像が映されており、見る意思にしたがって瞬時に視点を変えることができるのはこのためです。よって周辺の歪みもボケも、眼球は極めて不自然なものとしてとらえ、強い刺激を感じるのです。
バードウォッチング、スポーツ観戦等長時間使用する場合は特に眼に優しい光学系が大切なのです。光学系の優れた双眼鏡は、作動とその他の部分も平均的に優れた良い双眼鏡と見てよいのです。
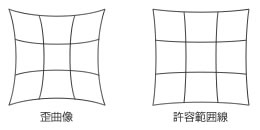
図8
【引用文献】
・光学技術ハンドブック (株)朝倉書店
・天体望遠鏡ガイドブック 誠文堂新光社
